Rを使ってIATにBayesian hierarchical diffusion modelを当てはめたい連載第2回です。今日はdiffusion model（拡散過程モデル）のお話をしようと思います。

diffusion model（拡散過程モデル）とは？

拡散過程モデルは、Ratcliff（1978）によって提案された、二肢選択分類課題（AかBかを判断する課題）における意思決定プロセスを推定するモデルです。反応時間データから、意思決定プロセスにおける情報を蓄積する速さや、判断の慎重さなどをそれぞれ推定することができます。

二肢選択分類課題では、「できるだけ速く、正確に」回答するように教示されることが多いですが、同一課題・同一参加者であっても、反応の速さを重視すれば正確性がおろそかになり、正確性を重視すれば速さがおろそかになってしまいます。また、課題を難しいと感じることで、正確性を上げようとより注意深く、慎重に課題に取り組むようになる傾向があります。さらに、社会的にセンシティブなテーマを扱う場合、実験参加者の心理的防衛が働きやすいため、課題を行うにあたって正確さを重視する戦略が取られる可能性もあります。

以上のような問題に対して、拡散過程モデルでは、反応するまでの意思決定の速さと反応の正確さを切り分けて考えることができるという点がメリットです。

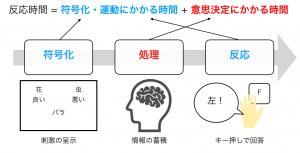
拡散過程モデルでは、上の図のように、データとして得られた反応時間は、刺激が呈示されてから《AかBかを判断するために必要な情報量が閾値に達した時間（上の図の「処理」）》と《刺激の符号化やキーを押すために手を動かす時間（上の図の「符号化」と「反応」）》によって生成されたものだと考えます。

土居・川西（2012）の図3がとても分かりやすいので、そちらをご覧ください。

土居・川西（2012）の図3の上についているヒストグラムは、正答したときの反応時間の分布で、下の方が誤答のときの反応時間の分布です。真ん中あたりからなみなみ伸びている線は、ある試行での情報処理プロセスです。このなみなみがたくさん終着したところが、ヒストグラムの頻度の高いところになります。そして、このなみなみの傾きが判断に必要な情報を蓄積していくスピードを表します。

判断に必要な情報を蓄積していくスピードがなぜなみなみで表されているのでしょうか。それは、拡散過程モデルでは、この情報蓄積のスピードが毎回毎回ランダムに変化する（「一次元Wiener過程」に基づく）と考えているからです。一次元Wiener過程は時間が経つにつれてランダム変化するものを説明する確率過程で、例えば、ブラウン運動（微粒子が不規則に運動する現象）の数理モデルに使われていたり、ホワイトノイズ（不規則なノイズ）の積分を表すのに使われているようです。拡散過程モデルでは、同じ刺激を呈示しても、試行によって反応時間が異なるのは、情報を蓄積するプロセスがこの一次元Wiener過程に基づくからだと考えています。

土居・川西（2012）の図3の縦軸の0とaは判断するのに必要な情報量の域値です。この0とaの間の距離が大きいほど、判断するために必要な情報量が多いことを示します。慎重に注意深く判断しようとすると、0とaの距離は大きくなります。また、0とaの間にあるzは初期値（スタートポイント）です。どちらの方向に反応しやすいかといった反応バイアスを示します。例えば、zがaの方に寄っている（近い）場合は、正解するのに必要な情報量が少ない、すなわち、正解の方向に反応しやすいことを意味します。

zの地点からなみなみが始まるまでの間にあるTerは刺激の符号化やキーを押すために手を動かす時間をまとめたもので、非決定時間と呼ばれています。

以上のように拡散過程モデルは、反応時間から主に4つのパラメーター（①判断に必要な情報を蓄積するスピード ②判断に必要な情報量の域値 ③反応バイアス ④符号化や運動に必要な時間）を推定することができます。これにより、反応時間そのままよりも詳細な情報処理プロセスがわかります。

拡散過程モデルの説明は、難波修史さんの楽しいスライドで見ることもできます。いつもお世話になっております。めっちゃ参考にしました。

今日はここまで。次回はIATに拡散過程モデルを当てはめている先行研究の紹介をしようかと思います。